The biggest remaining mystery in Apple’s M-series chips is their matrix co-processor, the AMX. Since early work by Dougall Johnson demonstrated their existence in the M1, this undocumented if not secret feature has been the subject of considerable research. Perhaps the best summary of that initial work is given in Johnson’s gist, and a compilation of additional information about the AMX instruction set available here. I’m not aware of any studies of the AMX in Apple’s latest M3 chips, and here set out to try to compare its performance with that of the M1, using the approach I’ve already applied to CPU cores.

After my first largely unsuccessful look at the AMX in an M3 Pro, I’ve regrouped and benefited from the advice of Maynard and Chad here (thank you). This article reports initial evidence from two new tests that I believe demonstrate the performance of the AMX in M1 Max and M3 Pro chips, and give insight into its management and power consumption.

Methods

Two new tests focus more closely on Accelerate functions that are most likely to be able to make use of the AMX, both involving matrix multiplication. They’re detailed in the Appendix at the end, complete with source code. Those loops were cast in code to ensure they’re run as separate threads, normally one thread to a CPU core; allocation to core type is then determined by the Quality of Service (QoS) assigned to each thread. Measurements were made of execution time, and CPU performance and power using powermetrics over 0.1 s sampling periods for up to 15 seconds.

Single-thread example

To demonstrate how those worked out, here are detailed results from one test, using sparse matrix multiplication at high QoS, thus running on the P cores of an M3 Pro.

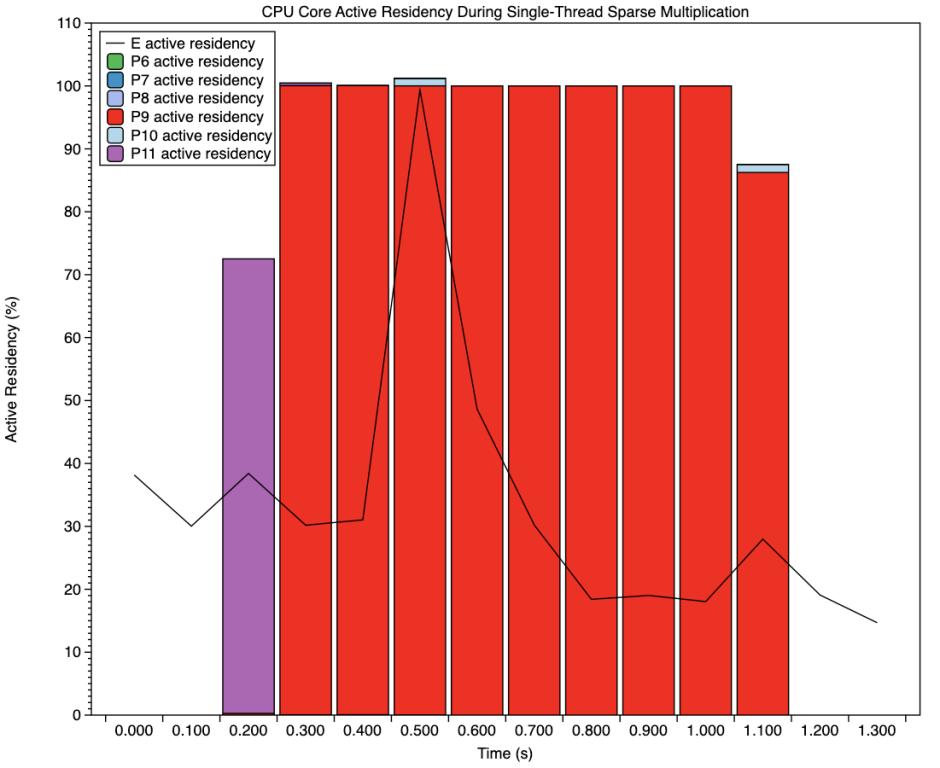
This chart shows core residency (100% means fully active without any idling) for each of the six cores in the single P cluster. For the 0.2 second periods shown before and after this test, there was no activity on the cores in that cluster. The first core to become active, CPU11, is shown in purple, apparently setting up the thread. CPU9, shown in red, then ran at 100% active residency, with no time spent idling, until the thread completed almost a second later. Other P cores showed only very small amounts of activity. The E cluster active residency is shown by the solid line; apart from a peak (at low frequency) at about 0.5 seconds, it showed little evidence of any involvement.

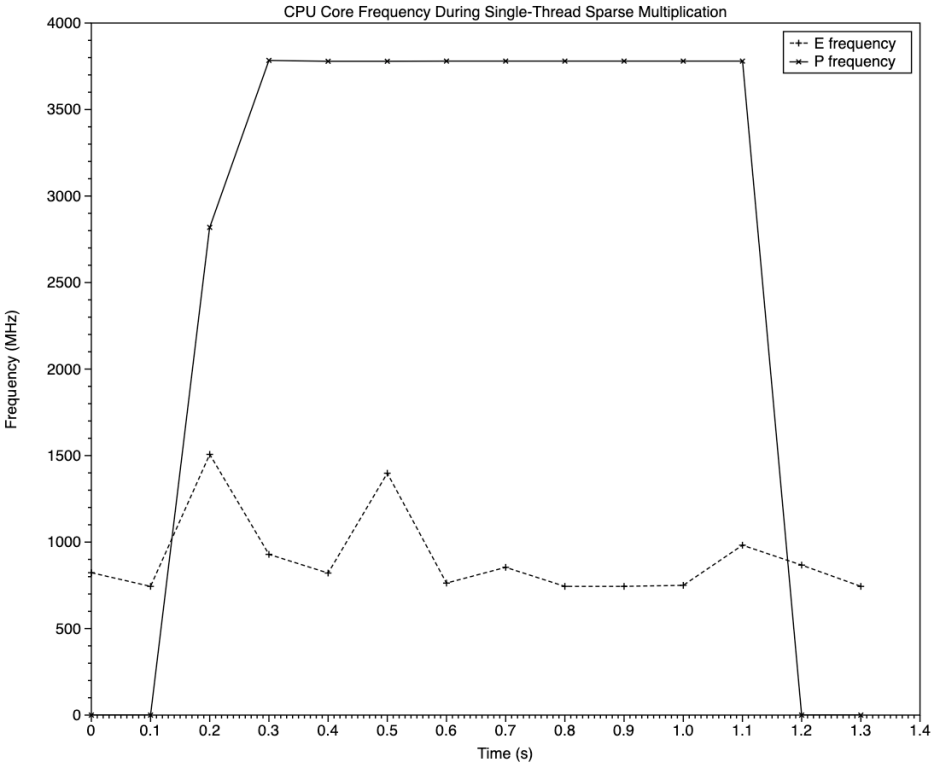
This chart shows cluster frequency over the test period. That for P cores, in the solid line, matches changes in active residency, running for the duration of the task at about 3800 MHz, a little below the maximum of just over 4000 MHz. E core frequency remained low throughout, much of the time below 1000 MHz.

If you’re familiar with my previous tests, these appear very similar, and you’re probably wondering what evidence there is of AMX use.

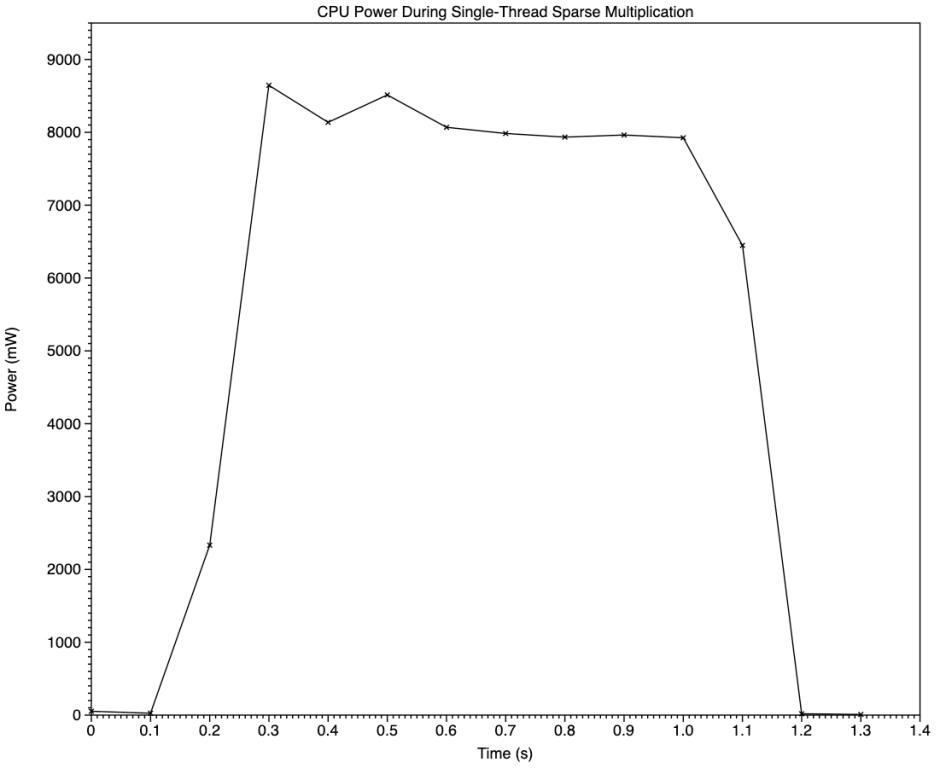
While the pattern of total CPU power use during the test is also similar, the Y axis is a complete surprise. To put this in context, at similar active residency and frequency, when running my floating point test on a single P core, the M3 Pro uses around 1000 mW, and when running NEON vector code it reaches 2500 mW. The plateau here at just over 8000 mW exceeds many of my previous multi-thread tests, although here it’s for just a single thread. Clearly, something very different is happening here, and this task isn’t being run on the NEON unit in a P core at all.

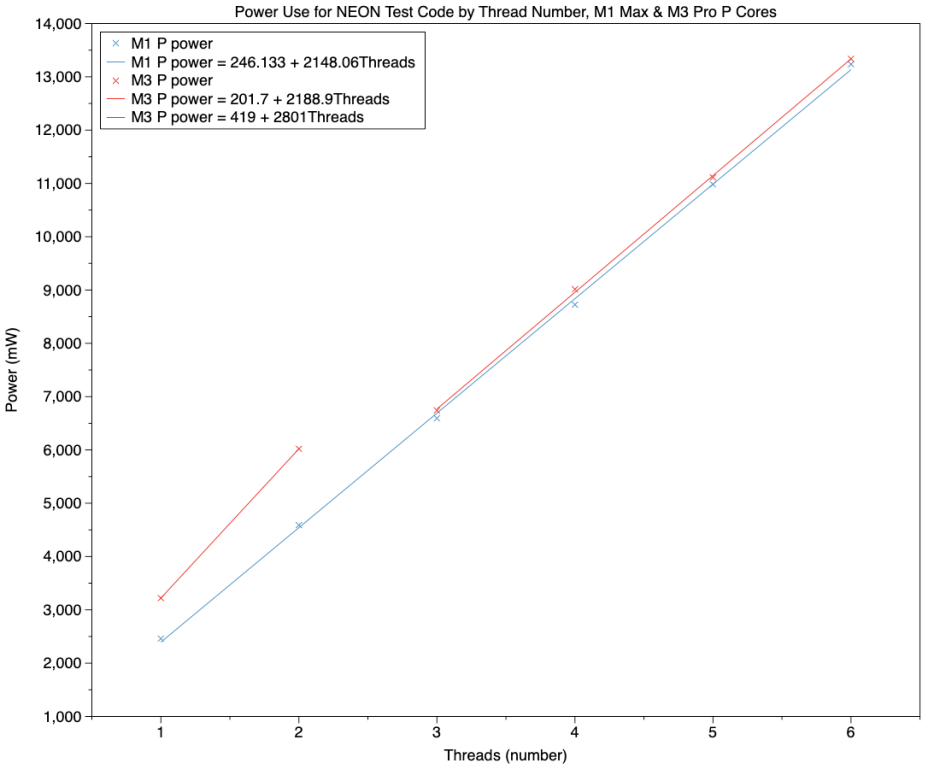
This chart from my previous NEON results adds more context. Similar power levels require more than three threads of 100% high frequency NEON processing. Although power measurements for the other test, of dense matrix multiplication, were slightly lower for a single core, at ‘only’ 5500 mW, they too support the idea that much of that power isn’t being used by the P core itself, but by something outside it.

As powermetrics also provides measurements of power use by the neural engine (ANE) and GPU, which both remained at or close to 0 mW, this matrix processing can only be accounted for with AMX involvement. Measurements from the M1 Max confirmed this, with single-thread sparse matrix multiplication reaching 4800 mW, compared with 2500 mW for NEON.

Multiple threads

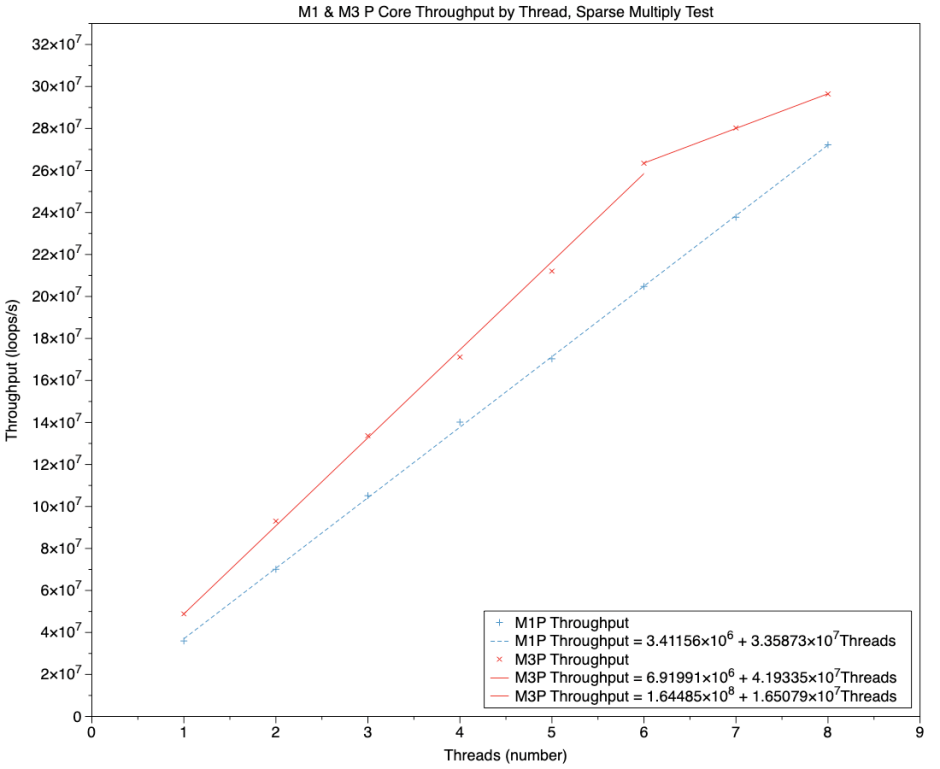
This chart shows test loop throughput by the number of threads, for both M1 Max (broken blue line) and M3 Pro (solid red line). As with previous equivalents, the M3 showed higher throughput for all tests, with the gradient of its regression line (up to its 6 cores) around 4.2 compared with 3.4 for the M1 Max, representing an improvement to 124% by the M3. The only discontinuity here is for the M3 Pro at six threads, above which additional threads are run on E cores, which still deliver respectable increases.

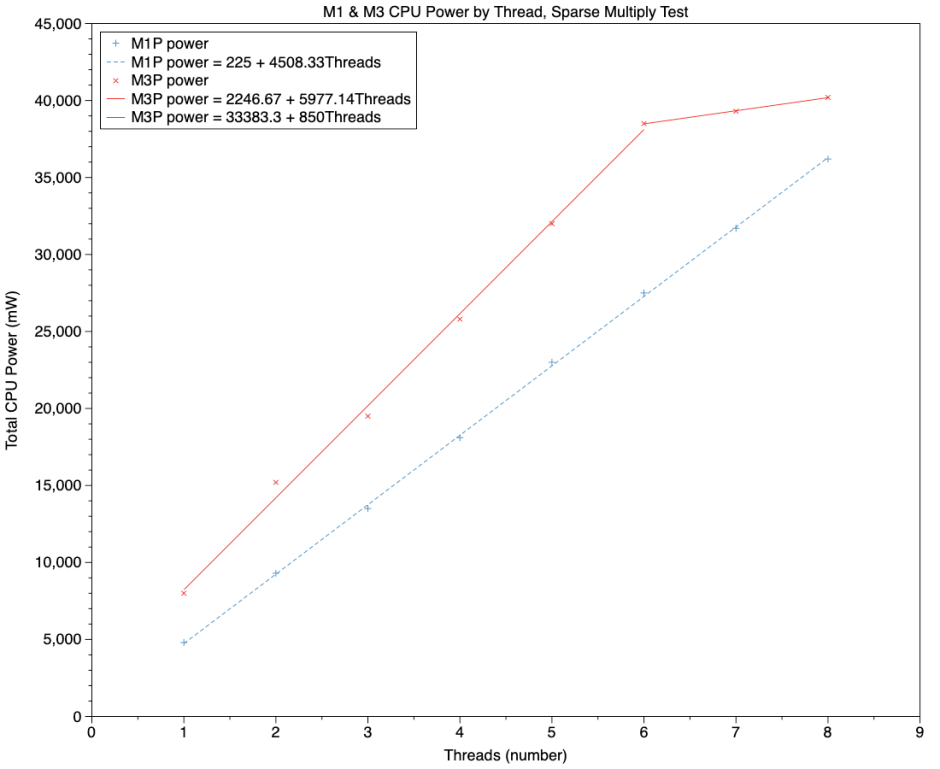
This chart shows power used, rather than loop throughput, and follows a similar pattern, with the M3 Pro using more power throughout. Adding each thread/core increased power used by 6000 mW for the M3 Pro, and 4500 mW for the M1 Max. Highest recorded total CPU power exceeded 40 W for the M3 Pro, and at six threads/cores was about 38 W, compared to a peak of less than 14 W for the NEON test on six cores.

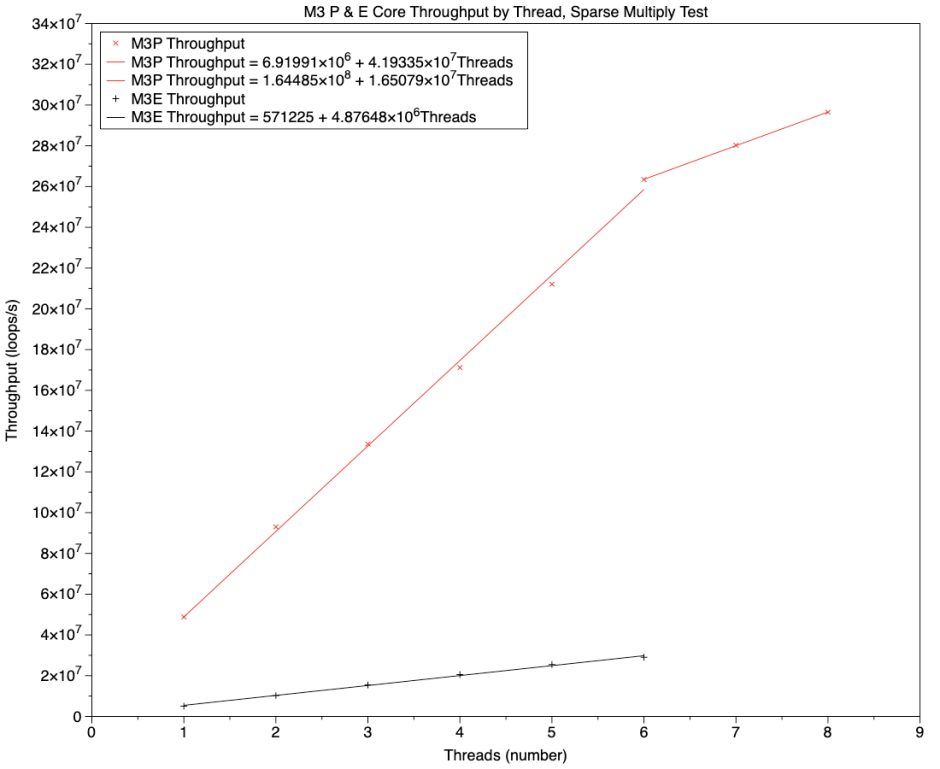
By comparison, the same tests run on the E cores of the M3 Pro use very little power, and reach far lower throughput as shown in this chart. P cores are shown in the red line, and E cores in the black line below. The gradient of the regression line for the P cores is 4.2 x 10^7 threads/s, and that of the E cores 0.5 x 10^7 threads/s.

Core allocation pattern

Further evidence that these tests involve the AMX comes from studying the patterns in which macOS allocates P cores. In all my other tests, this has followed a strict sequence, and is one of the strengths of these techniques.

When allocating these threads at high QoS, macOS first assigns them to P cores in the first cluster, until they are all running at high frequency and 100% active residency; it then starts allocating them to cores in the second P cluster, until they’re all at 100%, and finally to the E cores. In the matrix multiplication test (but not the sparse matrix multiplication) on the M1 Max, a different scheme emerged.

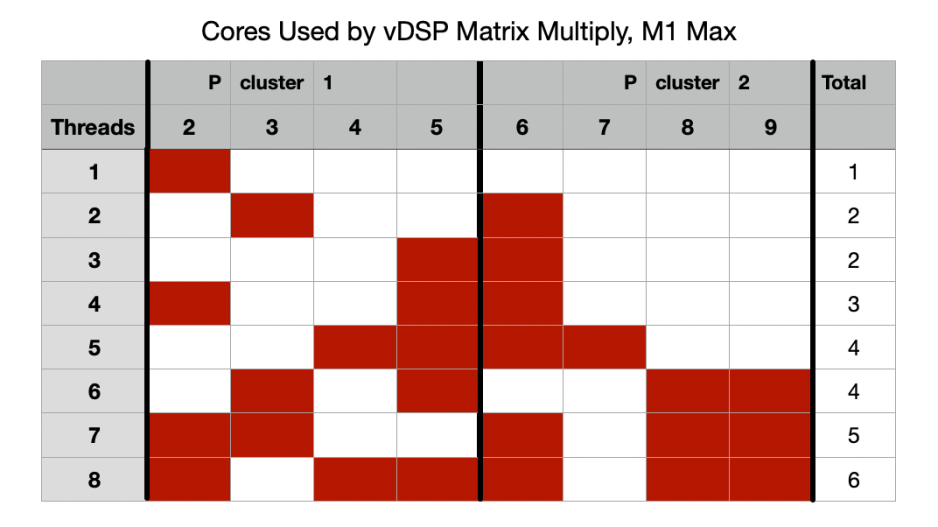
Red-filled cells here show the P cores used when running matrix multiplication threads at high QoS. There are two unique features that I have never seen in any of my previous tests:

• Instead of fully loading all cores in the first cluster before waking the second from idle, threads are allocated here to balance the load between the two clusters, and the second cluster was run up to high frequency and made active with the second thread, instead of the fifth.
• The number of active cores is less than the number of threads, for three and more threads. Given that the cores shown in white were idling almost the whole duration of testing (recall the bar chart above), this intentional under-allocation suggests that overall processing isn’t being limited by P core capacity, but by an external processing unit.

This supports the proposal that each CPU cluster has its own AMX co-processor, but it’s most likely that each larger cluster in an M3 still only has a single AMX, not two. However, the evidence here is that AMX performance has improved considerably since the M1.

Conclusions

• On Apple silicon Macs, code using vDSP_mmul() or SparseMultiply() in Apple’s Accelerate library will make use of AMX co-processor(s).
• If that’s correct, then total CPU power reported by powermetrics includes that of the AMX(es).
• If those are correct, then the AMX in an M3 Pro is considerably faster than that in an M1 Max.
• Measurements on the performance of the AMX for the E cluster confirm that it’s far slower and uses less power, than that of a P cluster.
• In some instances, macOS uses a distinctive pattern for allocating threads to balance the load between the two P clusters in an M1 Max, so as to balance load on their AMX co-processors. This can extend to under-allocating P cores.
• AMX power consumption can exceed that of the P cores.
• Although functions in the Accelerate library that make use of the AMX might appear to be unusual in apps, they may well be used in image and audio processing, and elsewhere. Do not underestimate their importance in the software we use now.

Postscript

In case you’re wondering just how much power an M3 Pro can use in its CPU, including AMX co-processors, running flat out I make that a peak of 44.5 W with all 12 cores at 100% active residency, although they weren’t running at maximum frequency. There’s still room for more!

Appendix: Source code

16 x 16 32-bit floating point matrix multiplication

var theCount: Float = 0.0
let A = [Float](repeating: 1.234, count: 256)
let IA: vDSP_Stride = 1
let B = [Float](repeating: 1.234, count: 256)
let IB: vDSP_Stride = 1
var C = [Float](repeating: 0.0, count: 256)
let IC: vDSP_Stride = 1
let M: vDSP_Length = 16
let N: vDSP_Length = 16
let P: vDSP_Length = 16
A.withUnsafeBufferPointer { Aptr in
B.withUnsafeBufferPointer { Bptr in
C.withUnsafeMutableBufferPointer { Cptr in
for _ in 1...theReps {
vDSP_mmul(Aptr.baseAddress!, IA, Bptr.baseAddress!, IB, Cptr.baseAddress!, IC, M, N, P)
theCount += 1
} } } }
return theCount

Apple describes vDSP_mmul() as performinng “an out-of-place multiplication of two matrices; single precision.” “This function multiplies an M-by-P matrix A by a P-by-N matrix B and stores the results in an M-by-N matrix C.”

Sparse matrix multiplication

var theCount: Float = 0.0
let rowCount = Int32(4)
let columnCount = Int32(4)
let blockCount = 4
let blockSize = UInt8(1)
let rowIndices: [Int32] = [0, 3, 0, 3]
let columnIndices: [Int32] = [0, 0, 3, 3]
let data: [Float] = [1.0, 4.0, 13.0, 16.0]
let A = SparseConvertFromCoordinate(rowCount, columnCount, blockCount, blockSize, SparseAttributes_t(), rowIndices, columnIndices, data)
defer { SparseCleanup(A) }
var xValues: [Float] = [10.0, -1.0, -1.0, 10.0, 100.0, -1.0, -1.0, 100.0]
let yValues = [Float](unsafeUninitializedCapacity: xValues.count) {
resultBuffer, count in
xValues.withUnsafeMutableBufferPointer { denseMatrixPtr in
let X = DenseMatrix_Float(rowCount: 4, columnCount: 2, columnStride: 4, attributes: SparseAttributes_t(), data: denseMatrixPtr.baseAddress!)
let Y = DenseMatrix_Float(rowCount: 4, columnCount: 2, columnStride: 4, attributes: SparseAttributes_t(), data: resultBuffer.baseAddress!)
for _ in 1...theReps {
SparseMultiply(A, X, Y)
theCount += 1
} }
count = xValues.count
}
return theCount

Apple describes SparseMultiply() as performing “the multiply operation Y = AX on a sparse matrix of single-precision, floating-point values.” “Use this function to multiply a sparse matrix by a dense matrix.”