Computers, particularly Macs, have revolutionised sound, music and audio. To achieve that, they have also transformed sound from an analogue world of instruments and sound waves into streams of digital data. This article helps you understand the fundamentals of digital audio.

Analogue sound, whether speech, music or ambient noise, consists of small pressure changes travelling as waves in the air. For the sake of example, I’ll start with the vibrating string of a musical instrument which is picked up by a microphone and transduced into an electric current, which varies according to a wave of the same pattern as in the air.

Before a computer can do anything with that electric current, it has to be converted from analogue form to digital, a stream of numbers, which is performed by an analogue to digital converter, or ADC, by means of rapidly sampling the input voltage.

Natural sound can range in frequency from almost nothing to medical ultrasound at several gigahertz in frequency. Thankfully, unlike some animals, humans have quite a limited range they can hear, typically from around 20 to 20,000 Hertz (20 Hz to 20 kHz). Ignoring any audio processing we might want to apply to the sound of our string instrument, to reproduce its sound faithfully we need to reconstruct its analogue waveform for audio output so that it’s identical to its input.

To achieve that, we must get two choices right: the sampling or conversion rate when converting from analogue to digital, and an appropriate precision for each of those sampled values. Get either of those wrong and the output will be distorted when compared to the original.

Sampling rate

Requirements for the sampling rate are the easier to determine, using the Nyquist-Shannon Theorem.

Just after the Second World War, Harry Nyquist and Claude Shannon discovered and proved that in order to reconstruct a waveform accurately you must sample the analogue waveform at a frequency of at least twice the maximum you need for reconstruction. So for normal human hearing, the lowest sampling rate which we can use is 2 x 20,000 = 40,000 Hz.

In practice, a little headroom is allowed, and the sampling frequency used for Audio CD was set at 44,100 Hz. More recently that has been replaced in most good quality digital audio systems by 48,000 Hz. But most sound and audio engineers prefer to work at twice that frequency, 96 kHz, before downsampling to 48 kHz for output.

It follows from the Nyquist-Shannon Theorem that digital audio sampled at 48 kHz is only capable of faithfully reproducing audio frequencies of up to 24 kHz. You couldn’t use that to record the ultrasonic sounds made by bats, or even many dog whistles. But is it sufficient to preserve the overtones and harmonics responsible for subtle properties such as timbre?

To understand that you need to understand how we hear sound.

Human ear

Our auditory transducers, the biological equivalent of ADCs, are hair cells contained in the Organ of Corti, in the cochlea, inside the inner ear. Depending on their position within the Organ of Corti, and the properties of the basilar membrane there, hair cells are highly sensitive to specific frequencies of sound. We know from abundant testing that few humans have hair cells capable of detecting sound at frequencies higher than 20 kHz.

Spectrum analysis

To see what frequencies might be involved in timbre, we need to resort to another eponymous analysis, that of Fourier. Using this, we can decompose the complex waveform generated by a musical instrument into a frequency spectrum, showing the frequency content of the sound.

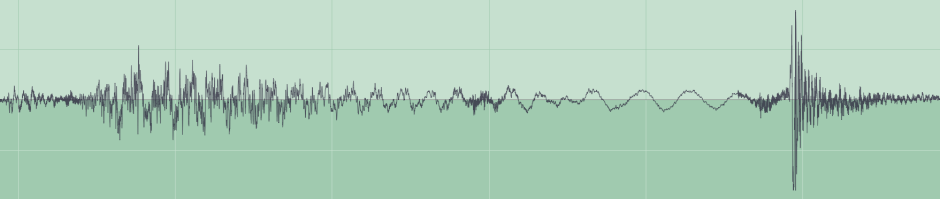
This sample contains a wide range of frequencies, which make up a complex series of different sounds.

Its frequency spectrum shows almost no power in frequencies above 16 kHz, and none at all above 22 kHz. Almost all the frequencies are in the audible range for humans, and according to the Nyquist-Shannon Theorem they could be faithfully represented by sampling at a frequency of at least 44 KHz. Using a higher sampling frequency of 48 kHz won’t preserve the original signal any better. Equally, humans are unable to distinguish between sound output from this at 44, 48 or 96 kHz.

Sampled values

In the early days of digital audio, sampled values obtained from continuous waveforms were stored as integers, and higher quality conversion used larger integer types. Single byte integers only have 256 different values, so the error in using them to represent continuous values is great. Early schemes simply used larger integer types to reduce the errors introduced by discretisation into integers.

More recently, with the advent of more capable processors, digital sound data has changed to using floating-point types, and the standard used internally in the Mac’s Core Audio currently employs 32-bit floating-point numbers for precise representation of digitised waveforms.

The combination of a sampling frequency of 48 kHz and 32-bit floating-point values ensures high fidelity in audio input and output, ample for human hearing to be unable to detect any difference.

Oversampling

While 48 kHz sampling is more than adequate to preserve all audio frequencies which can be heard by humans, wouldn’t it be preferable to sample at 96 kHz or more, to get even better quality?

Returning to the Nyquist-Shannon Theorem, sampling at 96 kHz rather than 48 kHz would add audio frequencies of 24-48 kHz, which can be heard by domestic pets and many other animals. Unfortunately, unless you buy very special audio equipment, you’ll discover that microphones and sound input devices, as well as headphones and speakers, simply can’t handle frequencies above 20 kHz, and in many cases their performance is already dropping off above about 17 kHz.

The penalty of oversampling is that, whatever you do with your digital audio data, there’s twice as much of it at 96 kHz as there is at 48 kHz. That may not seem much, but many computer algorithms don’t run in direct proportion to the quantity of data. Among those are some of the most important in audio processing, such as Fourier transforms. While fast Fourier transforms (FFTs) do better than scaling in proportion to the square of the data size, doubling the quantity of data still imposes significantly greater demands on your Mac’s processor. There ain’t no such thing as a free lunch when it comes to digital audio processing.

Nevertheless, most sound and audio engineers still opt for higher sampling rates than are necessary to generate perfectly good sound output for human ears. That’s a pro choice; for the rest of us there’s nothing to gain for the additional cost.

Reference

Apple’s extensive documentation starts here.